INTRODUCTION

In this blog, we will explore the mushroom dataset and use a Naive Bayes classifier to predict the edibility of mushrooms.

Importing Necessary Packages:

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

Reading the data:

mush=pd.read_csv('mushrooms.csv')

Exploratory Data Analysis(EDA):

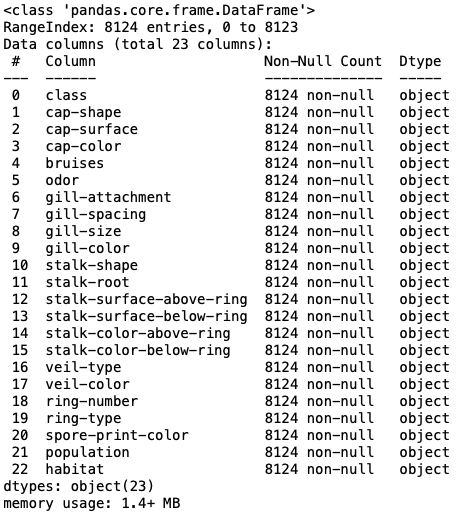
mush.info()

mush.columns

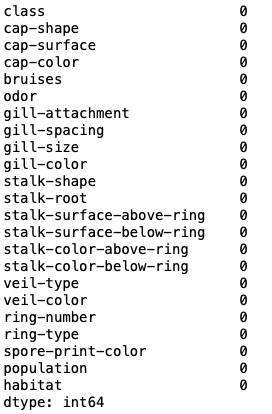
mush.isna().sum()

Statistical Inference:

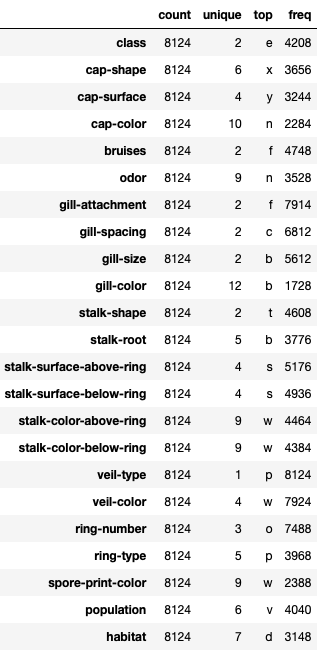
mush.describe().T

mush['class'].value_counts(normalize=True)

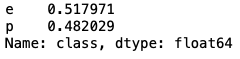
The mushroom dataset is fairly balanced in nature.

Here, we will build a Naive Bayes classifier to predict whether the mushroom is 'e' for edible or 'p' for poisonous.

Looking after the unique values in each columns of mushroom dataset:

for i in mush.columns:
    print(i,mush[i].unique())

mush['stalk-root'].value_counts(normalize=True)

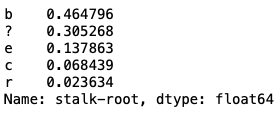
We can observe that the 'stalk-root' is a single column with '?' present in around 30% of its entries. Since 30% of the data represents a significant amount and cannot be removed from each column, the alternative is to remove the entire 'stalk-root' column.

Removing the stalk-root:

mush=mush.drop(columns=['stalk-root'])
mush.info()

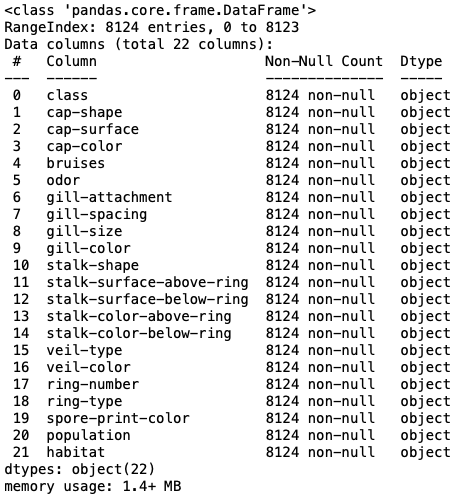The column-stalk root is removed.

Data Preparation:

#Input Features:
X=mush.iloc[:,1:]
print(X)

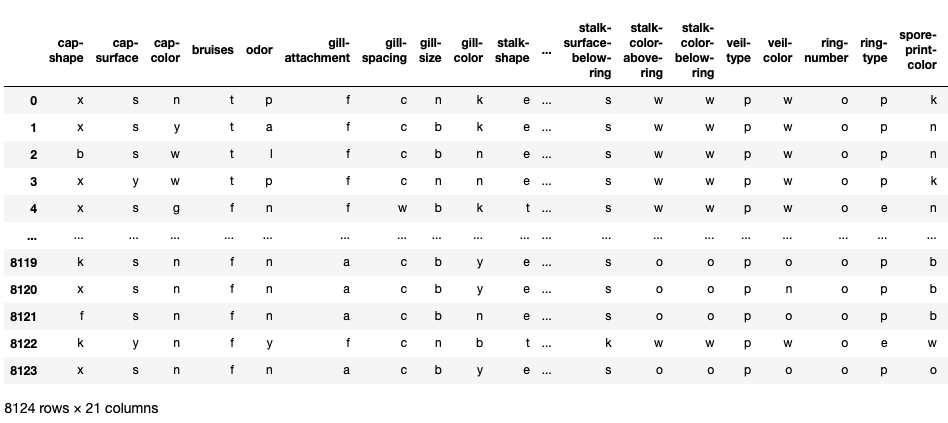
#Output:
Y=mush['class']
print(Y)

Since the inputs are categorical in nature, we need to convert them into numerical variables, as the Naive Bayes classifier deals with probability. We can achieve this conversion using 'get_dummies/Label Encoding.

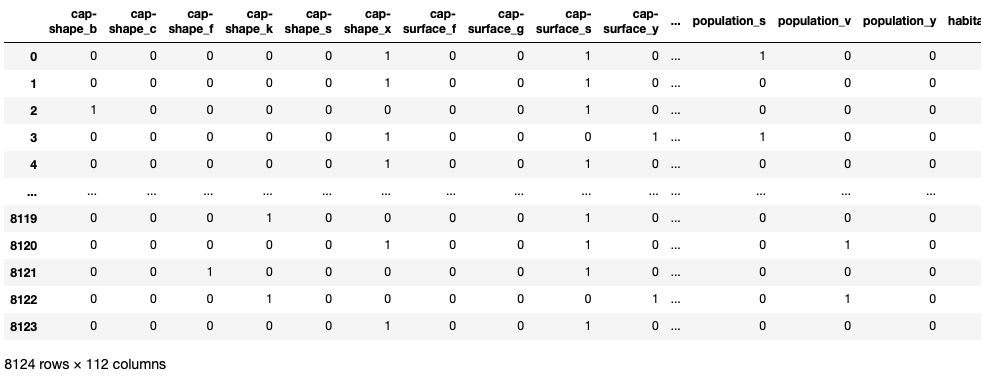
X=pd.get_dummies(X)  

The 'get_dummies' function operates by taking a DataFrame, series, or list and transforming each distinct element into a column header, subsequently assigning a value of 1 if there's a match and 0 if there isn't.

print(X)

Splitting the data into training and testing:

from sklearn.model_selection import train_test_split 
x_train,x_test,y_train,y_test=train_test_split(X,Y,test_size=0.3,random_state=1)
print(x_train.shape)
print(x_test.shape)
print(y_train.shape)
print(y_test.shape)
(5686, 112)
(2438, 112)
(5686,)
(2438,)

Training the model:

from sklearn.naive_bayes import GaussianNB
NB_classifier=GaussianNB()
NB_classifier.fit(x_train,y_train) 

Predicting the output:

y_pred=NB_classifier.predict(x_test)

Model Evaluation:

from sklearn.metrics import classification_report,accuracy_score,confusion_matrix
print(classification_report(y_test,y_pred))

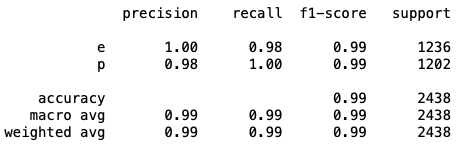
print(confusion_matrix(y_test,y_pred))
[[1216   20]
 [   2 1200]]
print(accuracy_score(y_test,y_pred))
0.9909762100082035  

Conclusion: This concludes our notebook. We used a Naive Bayes classifier from the scratch, trained it on our dataset, and observed an impressive accuracy of 99% during testing.