In this blog, we will look step by step at one of the most popular algorithm, i.e., AdaBoost classifier. We will also investigate the mathematics behind the algorithm.

Let’s look at a simple dataset.

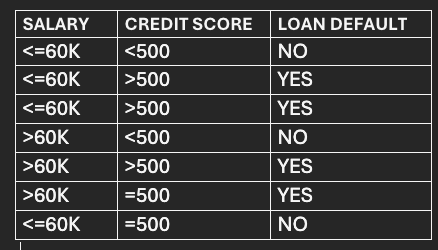
The data has 2 feature columns -Salary and Credit Score and 1 Target Column - Loan default. Based on the salary and credit score, we will be predicting whether the person defaulted on a loan.
Let’s understand how the Adaboost algorithm is applied to the above simple data.

STEP-1:

The first step of Adaboost algorithm is building a best decision tree stump.

A Stump is a simple decision tree with only one decision root node and two leaf nodes.

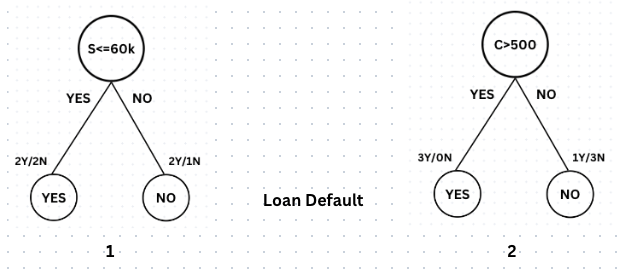
After creating various stumps, let's assume we end up with the above two stumps.

In the first Stump, the root node condition is 'Salary <= 60K'. If the condition is True, the leaf node has 2 instances labeled 'Y' (indicating loan default) and 2 labeled 'N' (indicating no loan default). If the condition is False, the leaf node has 2 instances labeled ‘Y’ and 1 labeled ‘N’.

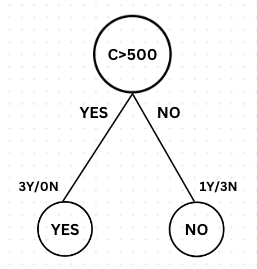
In the second Stump, the root node condition is C>500. If the condition is True, the leaf node has 3 instances labeled 'Y' and 0 labeled 'N'. If the condition is False, the leaf node has 1 instance labeled ‘Y’ and 3 labeled ‘N’.

Adaboost utilizes the concepts of Entropy, Information Gain, and Gini Index to determine the optimal or best Stump. The second Stump is superior of all stumps and will be selected by the algorithm since it has a pure leaf node (3Y/0N) and reduced randomness (1Y/3N) in the subsequent leaf node.

STEP-2:

Assign equal sample weights to each data point and utilize them with the initial model(M1), which is the Best Stump (2nd Stump), for making predictions.

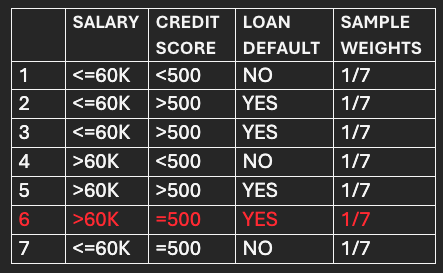
The Stump correctly classifies all the fed data points except the 6th numbered data point.
The total error of the Stump is 1/7 as it misclassifies 1 data out of 7.

The performance of the Stump or the weight(α 1) it contributes to the final classification is calculated by using the equation:
α 1=1/2log⁡e(1−Total Error/Total Error)
≈0.8921~0.9

STEP-3:

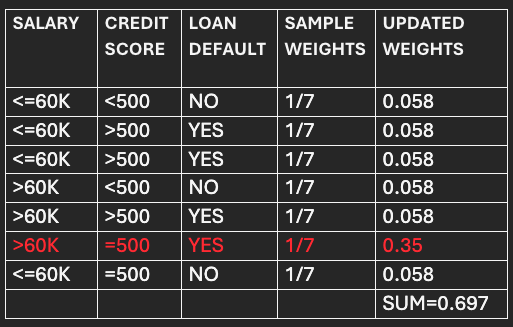
Update the weights for correctly and incorrectly classified data points.
For correctly classified points:
Updated weight=Sample weight * e-(α 1) =1/7 *e (-0.9) =0.058

For incorrectly classified points:
Updated weight=Sample weight * e(α 1) =0.35

We observe that the updated weights for the incorrectly classified points are significantly higher than those for the correctly classified points. Consequently, the succeeding model/stump will be given more attention to rectify previous errors.

STEP-4:

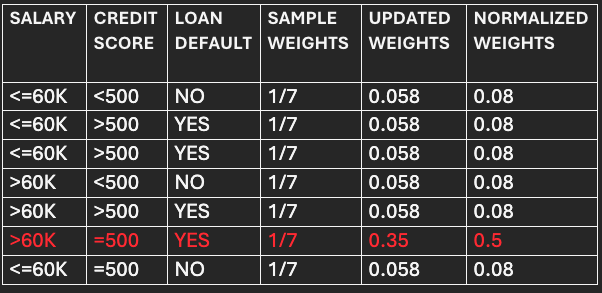
Computation of normalized weights and assignments of bins.

Normalized weights=Updated weights/Sum of Updated weights.

For correctly classified points:
=0.058/0.697
=0.083~0.08.
For incorrectly classified points:
=0.35/0.697
=0.5.
The normalized weights become the new sample weights for the succeeding model/Stump.

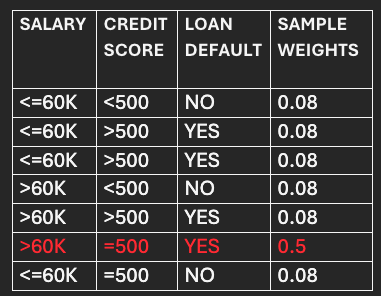
So, the data frame to be used for selecting data points for the next model/stump (M2) will look like the following:

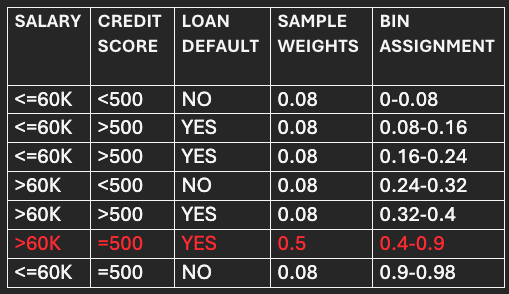
Now the bins are assigned to each data point based on their normalized or new sample weights.
After assigning bins, the data frame will look like below:

The next immediate question that arises is the use case of bins and how the data points are selected for the succeeding model. We will look at the next step.

STEP-5:

Run a For Loop to generate a random number between 0 and 1. The record following the bin where the generated random number falls will be chosen for the next model.

Let’s say the random numbers generated are (0.5,0.1,0.6,0.7,0.22,0.3,0.87).

The bin size of the incorrectly classified point is 0.5, significantly higher than the bin size of correctly classified points (0.08). As a result, most of the time, the randomly generated number falls into the bin of incorrectly classified points, leading the algorithm to focus more on previous model's incorrect predictions.

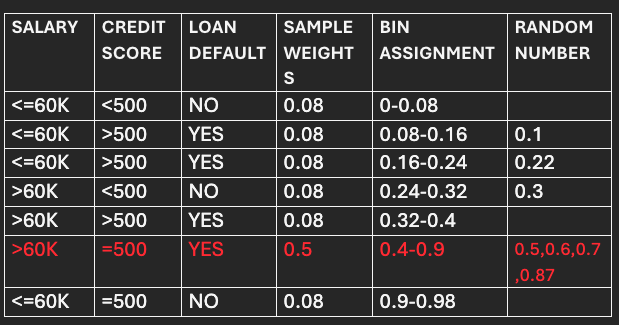
The incorrect record is selected 4 times, while the rest are selected only once for the next model/stump.
Steps 1 to 5 are repeated to build the best model/stump using Entropy, Information Gain, and Gini Index and the incorrectly classified points are emphasized more when passing the data sequentially to the next model.

STEP-6:

Predict all the given test data.

Let's assume that the Adaboost algorithm has sequentially built models M1, M2, M3, and M4 with confidence/weights: α1=0.9 for 'Yes', α2=0.65 for 'No', α3=0.24 for 'Yes', and α4=-0.3 for 'No'

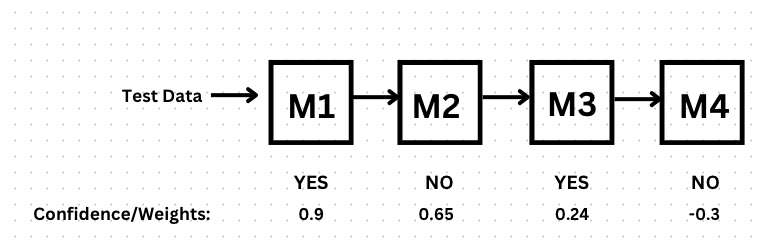Let's say we have to predict the data (<=60K,>500):

Output of Adaboost will be:

=0.9(Yes)+0.65(No)+0.24(Yes)-0.3(No)

=1.136(Yes)+0.35(No)

As the confidence/weight for 'Yes' is greater than that for 'No' when combined sequentially, the algorithm's output will be 'Yes'.