NAIVE BAYES CLASSIFIER

Introduction

Naive Bayes classifier is a probabilistic supervised machine learning algorithm used in classification problems. The term ‘Bayes’ refers to the Bayes theorem and ‘Naive’ refers to the assumption of independence among the features(columns), which means that changing a feature's values doesn’t change the value of another feature. In real-world scenarios, it is uncommon where the features are independent. But, then why this algorithm is so popular and famous?

In this blog, we will discuss the significance of Naive Bayes and explore the prerequisite mathematical concepts employed in probability and conditional probability. Additionally, we will deep dive into the concept of Bayes' theorem, which aids in understanding the Naive Bayes algorithm.

Table Of Contents:

• Independent/Dependent events.
• Conditional Probability & Bayes Theorem.
• Naive Bayes in classification.
• Tennis dataset example.
• Advantages of Naive Bayes.
• Assumptions & Disadvantages in Naive Bayes.
• Conclusion.

Independent Events

Independent events in probability refer to events that don't affect or impact each other. In other words, the occurrence or non-occurrence of one event does not affect the probability of the other event happening.

For example, tossing a fair coin. Each coin toss is an independent event because the outcome of one toss doesn’t affect the outcome of subsequent toss. Each toss has a 50% chance of getting head and a 50% chance of getting tail, regardless of the previous toss.

Mathematically, two events A and B are considered to be independent if:

$P(A \cap B) =P(A)*P(B)$

Dependent Events

Dependent events in probability are events that are influenced or affected by each other. The occurrence or non-occurrence of one event has an impact on the probability of the other event happening.

For, example consider a bag containing 5 marbles-3 red and 2 green marbles. Given that the first one is red, what is the probability of getting green?

In the first event(A) the probability of getting a red marble will be P(R)=3/5.

In the second event(B) the probability of getting a green marble given the first one is red will be P(G/R)=2/4.

Conditional Probability and Bayes Theorem

For a given events A and B, The probability of A and B which means first event A and then the event B has occurred is given by: P (A and B) = P(A) * P(B/A) --Equation (1) (Since A and B are dependent events)

where P(B/A) is the ‘conditional probability’ which is the probability of event B occurring given the ‘condition’ that event A has already occurred.

Conditional probability is the probability of an event occurring given that another event has already happened.

P (A and B) = P (B and A) -- Equation (2) (Commutative Property) From Equation 1, we can write the Equation (2) as: P(A) * P(B/A) = P(B) * P(A/B) --Equation (3)

On simplifying, we get

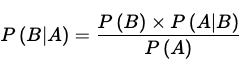
--Equation (4) which is the Bayes theorem.

Here, we are interested in finding P(B/A), which represents the probability of event B given the evidence of event A. This probability is also referred to as the "posterior probability".

we call P(B) the "prior probability," which means it is the probability of an event before considering any evidence.

P(A|B) is referred to as the "likelihood," while P(A) is known as the "marginal likelihood."

Naive Bayes in classification

Bayes theorem is used extensively in the Naive Bayes Classifier for predicting the output/class of the given test data. we will understand how the Bayes theorem is applied in supervised machine learning classification algorithms.

In a classification machine learning algorithm, we have $x_1, x_2, x_3, x_4 ….x_N$ features and a categorical output variable Y(yes/no).

We can write the Bayes equation for the above classification problem as:

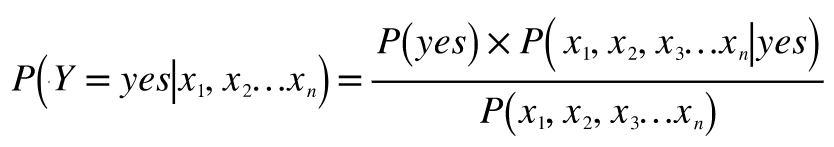
Equation (5)

Since we have assumed independence among the features, we can write Eqn-5 as:

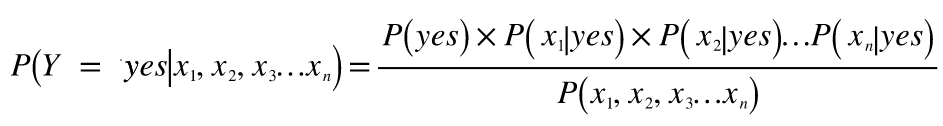
Equation (6) gives us the probability of the output Y=yes or 1.

Similarly, the probability of the output Y=no or 0 will be:

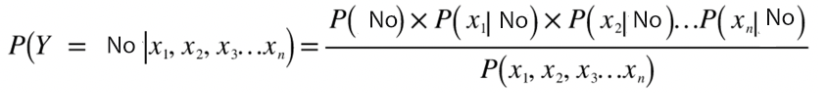
Equation (7) The denominator in equations (6) and (7) is the same and can be considered as constant. The output Y will belong to either class Yes or No, which will be determined by the highest probability among the two equations(6) &(7).

Tennis Example:

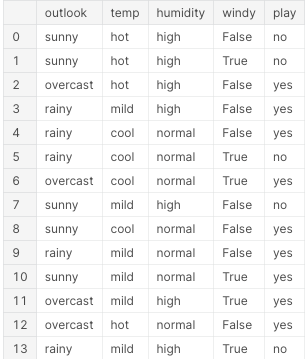
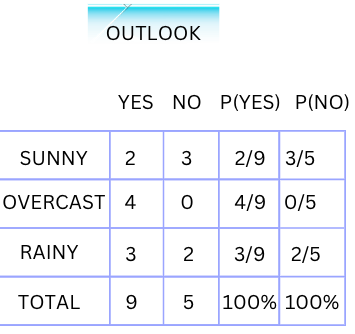
The probability of Yes and No with respect to individual attributes (Sunny, Overcast, Rainy) in the feature (Outlook) will be:

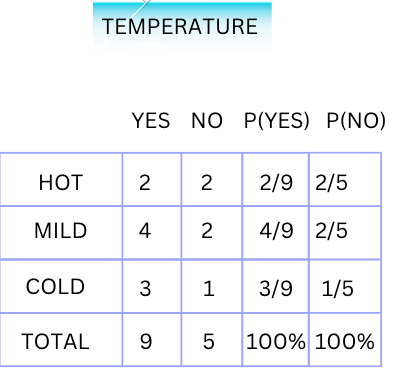
Similarly, the table for feature Temperature will be:

Now, let's suppose we have to predict whether the output Y=Yes/No given the weather condition is (Sunny and Hot). We have $x_1$=Sunny and $x_2$=Hot.

From equation (6) The probability of Y=Yes, or that the person will play tennis given the weather conditions (Sunny, Hot) can be written as

P (Y=Yes/Sunny, Hot) = P(Yes)*P(Sunny/Yes) *P(Hot/Yes)

= (9/14) * (2/9) * (2/9) = 2/63 = 0.031.

Similarly, from equation (7) The probability of Y=No, or that the person will not play tennis, can be written

P (Y=No/Sunny, Hot) =P(No)*P(Sunny/No) *P(Hot/No)

= (5/14) * (3/5) * (2/5) =3/35=0.085.

The % of P(Y=No) =0.085/ (0.031+0.085) = 73% The % of P(Y=Yes) will be 0.031/(0.031+0.085) = 27%.

Since the percentage of P(Y=No)>P(Y=Yes), the output Y will be ‘No’ or the person will not play tennis.
This is exactly how the Naive Bayes classifier helps in the prediction for classification problems.

Advantages of Naive Bayes

• Fast and efficient training and prediction process(Probabilistic approach).
• Works well with high-dimensional datasets.
• Performs well with a small amount of training data.
• It is used in applications like text classification, weather prediction, sentiment analysis etc.

Assumptions & Disadvantages in Naive Bayes

• Assumes independence among features, which may not hold true in real-world scenarios.
• Assumes that the features follow a normal distribution.
• May result in biased predictions if the input features are strongly correlated.
• Limited ability to capture complex relationships in the data.

Conclusion:

Naive Bayes classifier is a simple and efficient probabilistic algorithm used for classification tasks, relying on the Bayes theorem. It has advantages such as fast computation, handling high-dimensional data, and works well with small datasets. However, its assumption of feature independence can limit its accuracy in complex scenarios.

You can refer to the "Hands-on & Projects" sections on my website, where we will demonstrate the implementation of the Naive Bayes classifier using Python.