Logistic Regression

In the previous blog, we discussed some of the basic concepts in linear regression, types of linear regression, cost function, and performance metrics. In this blog, we will learn some of the basic concepts of logistic regression. Let's get started by going through the introduction of logistic regression.

Content

• Introduction
• Types of Logistic Regression
• Why logistic instead of linear Regression?
• Linear Regression vs logistic regression.
• Applications of logistic regression.
• Conclusion.

Introduction

Logistic Regression is a popular machine learning algorithm which comes under the wing of ‘Supervised Learning’. It is one of the predictive modelling techniques used whenever the dependent variable(Y) is categorical in nature like whether the person is diabetic or non-diabetic, whether the mail is spam or not spam etc. The inputs (features/independent variable(X)) can be continuous or discrete in nature.

It is one of the tools for applied statistics and discrete data analysis. It gives predictions/outcomes for the dependent variable(Y) in terms of probability. Based on a particular threshold/cutoff for the probability we will be able to classify the given data points. Threshold/cut-off probability is also known as decision boundary which helps in classifying the data points.

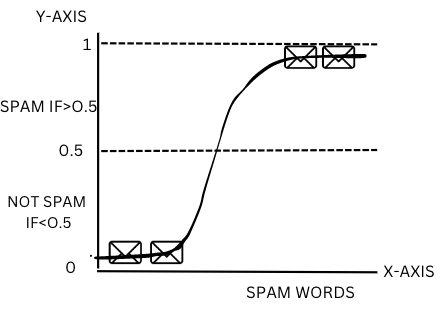
Ex:- If the probability of a mail being spam for a given set of inputs/features (count of spam words like cash bonus, double income, guaranteed, million dollars) is 0.6, which is greater than the default threshold probability of 0.5, then we will classify the mail as spam (1). Similarly, if the probability of a mail being spam is 0.4, which is less than the default cut-off probability of 0.5, we will classify the mail as not spam(0).

Types of logistic regression

1.Based on the number of independent variables(X):

• Simple Logistic Regression: In simple logistic regression, there is only one independent variable (X) used for predicting the output (dependent variable Y).

• Multiple Logistic Regression: In multiple logistic regression, there are more than one or we can say multiple independent variables (X) used for predicting the output (dependent variable Y).

2.Based on the number of Classes of dependent variables(Y): -

• Binomial/Binary Logistic Regression: The target (output variable) has exactly two categories (classes) such as 0/1, Yes/No, Spam/Not Spam, etc.

• Multinomial Logistic Regression: The target (output variable) has three or more categories(classes) unordered in nature like cats, dogs, sheep, etc.

• Ordinal Logistic Regression: The target (output variable) has three or more than three categories(classes) which are ordered in nature like low, medium, high etc.

Why do we need logistic regression instead of linear regression?

We know that linear regression is used when we have a continuous target/output variable. But why can’t we use the linear regression algorithm for discrete/categorical target variables? Why do we use logistic regression instead?

Let us try and understand this with the help of a simple logistic regression example: -

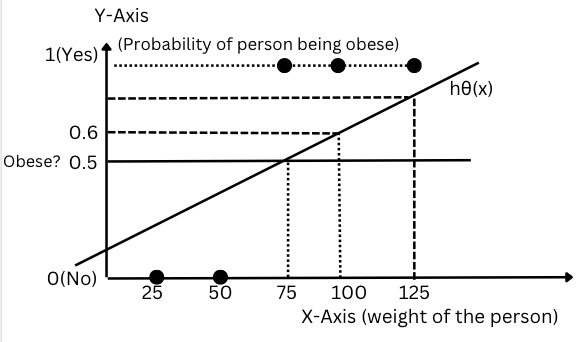Figure-(2)

In the above graph, the input variable (X) is weight, and we are trying to predict the output, which is categorical in nature indicating whether the person is obese or not obese.

Let us try and solve this categorical problem using a linear regression line given by

$h_\theta$(x) = $\theta_0$+$\theta_1$ * X or Y=mx+c

Where: $-\theta_0$=Intercept, $\theta_1$=Slope, X=input and $h_\theta(x)$=linear regression line.

The range of the output is either 0 or 1. Let us consider a threshold/cut-off probability of Y as 0.5. From the linear regression line, it is clear that any person with a weight greater than 75kg has a Y value greater than or equal to 0.5(Threshold probability) and is considered obese, or Y=1.

Mathematically speaking:

If: $h_\theta$(x)>=0.5, then the person is obese or Y=1

Else: $h_\theta$(x)<0.5, then the person is not obese or Y=0.

Here, we are able to solve a classification problem using the linear regression line $h_\theta(x).$ However, why do we need logistic regression? Why is logistic regression necessary, even when we have the linear regression algorithm?.

Let us analyse the graph below with an outlier, and we will be able to answer those questions.

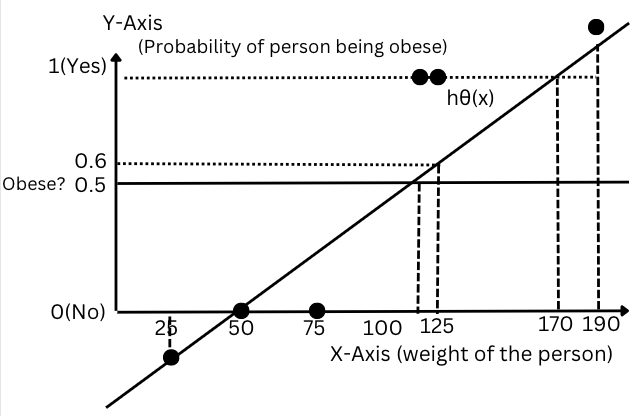Figure-(3)

Imagine we now have an extra data point, which is an outlier (~190 kg). To obtain the best-fit line (or minimum sum of squared errors), the linear regression line changes its orientation and shifts slightly towards the right side so that the distance of all the data points w.r.t to the line is minimum implying MSE is minimum.

we can see from the new linear regression line that we are classifying the person with a weight of 75 kg as not obese(since it is less than the threshold probability 0.5 of the new linear regression line) which is an error. The new regression line is completely different(~120kg weight has 0.5 threshold probability now) and changed as compared to the previous linear regression line classification. Thus, with the inclusion of a single outlier, the error has significantly increased due to the misclassification of many data points by the new regression line.

Secondly, we can see that from the regression line for all the persons having a weight greater than ~170kg we have the value of Y>1 and similarly for all the persons having a weight less than 50kg, we have the value of Y<0. These points are considered as ambiguous as we don’t know how to classify them.

In summary, we considered logistic regression over linear regression because:

1. The linear regression line doesn’t work well with the outliers. With the presence of outliers, the misclassification will increase and hence the errors will be increased significantly.

2. In logistic regression we convert the continuous linear regression line to an S-curve using the sigmoid function, which will always give values between the range of ‘0 and 1’ helping us to classify all the data points.

Linear Regression vs Logistic Regression

Linear Regression	Logical Regression
Linear Regression is used for regression problems.	Logical Regression is used for calculation problems.
Linear Regression is used for predicting continuous dependent variable	Logical Regression is used for predicting categorical depended variable.
In Linear Regression, we find the best fit linear line	In Logical Regression, we find the best fit sigmoid curve
MSE, or Mean Squared Error is cost function	MLE, or Maximum Likelihood Estimation is cost function

Applications of logistic regression:

• Medical diagnosis.
• Spam Detection.
• Credit Risk Analysis.
• Fraudulent Detection.

Conclusion

In conclusion, logistic regression is a supervised learning algorithm used for solving classification problems. The dependent variable can be binary (0/1) or multi-class in nature (Ex: Cat, Sheep, Dog). Logistic regression gives predictions for the dependent variable(Y) in terms of probability. Based on a particular threshold/cutoff for the probability we will be able to classify the given data points. Logistic Regression has wide applications in medical diagnosis, spam detection, credit risk analysis and many more.

In my next blog, we will look in-depth at the sigmoid function, cost function and maximum likelihood estimation in logistic regression.